2.2. Comunicación de Resultados Numéricos para la Toma de Decisiones Compartida
Laura Diego, Ricard Meneu, Lucía Prieto, Pedro Rey-Biel
2.2.1. Introducción: Competencia Aritmética en Salud
La alfabetización en salud ha sido definida por la Biblioteca Nacional de Medicina (NLM) como el «grado en que las personas tienen la capacidad de obtener, procesar y comprender la información y los servicios básicos de salud necesarios para tomar decisiones de salud apropiadas»1. Para el Instituto de Medicina de los Estados Unidos (IOM) la alfabetización en salud incluye una variedad de habilidades más allá de la lectura y la escritura, que incluyen la competencia aritmética (numeracy), la comprensión auditiva y la expresión oral, basada en el conocimiento cultural y conceptual2.
Los usuarios de la información relacionada con la salud, como pueden ser profesionales sanitarios, pacientes, familiares, gestores, decisores o incluso periodistas, tienen a menudo dificultades para comprender el significado de las estadísticas sobre salud y su representación gráfica, de lo que pueden terminar derivándose conclusiones erróneas y decisiones no óptimas. La evidencia científica muestra que los problemas con la competencia aritmética son comunes entre todos los agentes, se originan por un marco no transparente de la información, tanto de carácter no intencional (atribuible a problemas de comprensión, como, ocasionalmente, resultado de esfuerzos intencionados para manipular o persuadir) y que puede tener graves consecuencias para la salud3.
2.2.1.1. ¿Se interpreta adecuadamente la evidencia disponible?
Para comunicar y procesar de modo adecuado los resultados conocidos es preciso comprenderlos correctamente. Sin embargo, no es la comprensión un problema que radique únicamente en los receptores de la información, sino que incluso los profesionales sanitarios muestran con frecuencia dificultades para interpretar de manera apropiada resultados estadísticos sencillos4.
Sirva de ilustración el citado estudio4, descrito con más detalle posteriormente, en el que a 160 ginecólogos alemanes se les facilitó el valor de la prevalencia, la sensibilidad y la tasa de falsos positivos de una prueba de cribado de cáncer, pidiéndoles que señalasen la probabilidad de que una mujer sometida a la misma fuese un verdadero positivo. Las opciones de respuesta eran 1%, 10%, 81% y 90%. Solo el 21% de los participantes señaló la respuesta correcta (10%) mientras el 60% optó por las opciones que sobrestimaban abultadamente. Especialmente preocupante resultó la variabilidad apreciada, conviviendo estimaciones del 1% con otras tantas del 90%. El ejemplo es especialmente alarmante por el hecho de que quienes interpretaban incorrectamente información estadística relativamente sencilla, eran precisamente los especialistas habituados a trabajar con ella, los que a su vez eran los responsables de transmitirla y de guiar la decisión sobre hacer pruebas de cribado o sobre el tratamiento a seguir por los pacientes en el caso de que la prueba fuera positiva.
Un experimento más complejo5 evaluó la comprensión de médicos residentes sobre la evidencia que se les presentaba acerca del cribado de cáncer y su recomendación al paciente, así como sus creencias a priori, su competencia aritmética, nivel de alfabetización científica, conocimiento de las estadísticas sobre cribado y formación en estadística y demografía. El estudio demostró que la comprensión de las estadísticas de detección del cáncer y la capacidad de inferir los beneficios potenciales para los pacientes son esenciales para las recomendaciones basadas en la evidencia. Sin embargo, los autores del trabajo apuntan que las fuertes creencias a favor del cribado, favorecidas por las campañas de promoción, pueden influir en la forma en que los médicos procesan la evidencia sobre evaluaciones específicas, mostrando una mayor proclividad hacia el cribado que la avalada por la evidencia.
Los sesgos cognitivos más comunes, descritos en esta sección, pueden influir en la precisión diagnóstica o inducir a errores en el manejo clínico. En una revisión sistemática de los estudios realizados sobre médicos, utilizando viñetas de casos o escenarios reales se identificaron diecinueve sesgos cognitivos. El exceso de confianza, el efecto de anclaje, los sesgos de información y disponibilidad, así como la tolerancia al riesgo son los sesgos que más se asocian a imprecisiones en el diagnóstico o al manejo subóptimo de los casos5.
2.2.1.2. ¿Existe evidencia de que una mejor interpretación numérica mejora el proceso de toma de decisiones?
Como se muestra a continuación, la baja capacidad numérica puede distorsionar las percepciones de los riesgos y los beneficios de los cribados, reducir el cumplimiento de la medicación, impedir el acceso a los tratamientos, deteriorar la comunicación de riesgos y, a partir de la escasa investigación realizada sobre resultados, incluso afectar negativamente a los mismos. También se asocia con una mayor susceptibilidad a factores ajenos a la toma racional de decisiones, como los efectos del estado de ánimo, la forma en la que se presenta la información, y a sesgos en el juicio y en el marco de la toma de decisiones v.gr., encuadre y efectos de sesgo de relación6.
En general, la baja alfabetización en salud se asocia con un aumento de las hospitalizaciones, un mayor uso de servicios de urgencias, menor utilización de mamografías y vacunación antigripal, problemas con el cumplimiento de los tratamientos o una menor capacidad para interpretar los prospectos y los mensajes de salud. Los factores más importantes observados entre los individuos con menor capacidad para interpretar la información numérica son la edad, el peor estado general de salud o la pertenencia a grupos con tasas de mortalidad más altas7.
A continuación, se muestran algunos ejemplos, fundamentalmente provenientes de estudios con diseño experimental, de la relación mostrada entre competencia aritmética (numeracy) y resultados en salud. Igualmente, se presentan algunas soluciones tanto para facilitar la comprensión numérica como para presentar información gráfica de una forma en la que sea más sencilla de comprender, menos proclive a interpretaciones causadas por sesgos cognitivos, y con menos capacidad de manipulación de la decisión compartida. No obstante, aún a día de hoy los estudios de este tipo son relativamente escasos8 y los resultados encontrados muestran cierta inconsistencia. Por ello, aunque aún es necesaria más investigación, creemos que los siguientes ejemplos son lo suficientemente robustos para ofrecer unas primeras directrices sobre cómo los diferentes formatos en los que se presenta la información pueden afectar a la percepción de los riesgos, persuadiendo a que los pacientes tomen decisiones no necesariamente óptimas.
2.2.2. Uso de ayudas visuales para mejorar la comunicación de datos numéricos
Las ayudas visuales son representaciones gráficas de datos numéricos que pueden utilizarse para facilitar la comprensión de las probabilidades de un evento8,9,10. Por esta razón facilitan la toma de decisiones informada a profesionales sanitarios, pacientes o usuarios11,12,13,14.
2.2.2.1. Aspectos clave en el uso de ayudas visuales
En la utilización de las ayudas visuales para la comunicación de datos numéricos, se deben tener en cuenta aspectos referentes al receptor de la información, como su capacidad para comprender la información gráfica, aspectos referentes al objetivo de la comunicación y al diseño de la propia herramienta.
La capacidad de los individuos para comprender la información gráfica, hacer inferencias y sacar conclusiones de la misma se resume en el nivel de competencia gráfica (graph literacy). Los individuos con un nivel bajo de competencia gráfica tienen más probabilidades de ignorar los elementos más relevantes de una ayuda visual15 e interpretar, por tanto, erróneamente las representaciones visuales16, en comparación con las personas que cuenten con un mayor grado de esa competencia. No obstante, los factores que determinan el nivel de competencia gráfica no están claros18, aunque pueden compensarse, parcialmente, mediante el uso de ayudas visuales adecuadamente diseñadas. Para esto, hay que tener en cuenta ciertas consideraciones generales de diseño, así como el tipo de gráfico escogido19.
2.2.2.2. Consideraciones generales para el diseño de ayudas visuales
En el diseño de ayudas visuales es conveniente evitar los mensajes o representaciones ambiguas y engañosas, ya que la disposición de la información en un gráfico puede conducir así a una interpretación errónea. Por ello, es conveniente seguir ciertas normas básicas:
- Utilizar títulos y descripciones claras.
- Utilizar un lenguaje sencillo, que resulte comprensible y familiar al receptor.
- Incluir los mensajes clave en las descripciones de las ayudas visuales.
- Proporcionar la escala de medida y utilizar la misma escala de medida al presentar comparaciones.
- Evitar los gráficos truncados. Se trata de gráficos en los que uno de sus ejes, o ambos, no empiezan desde cero. Los gráficos truncados son aquellos cuyos ejes de datos están seccionados, de manera que solo se muestra el rango de datos posibles en el cual hay información. Un ejemplo de gráfico truncado se puede ver en la figura 2.2.1.
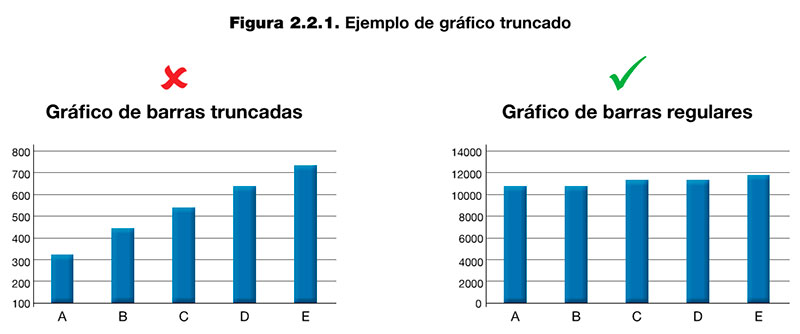
Por otra parte, es aconsejable evitar información innecesaria o elementos superfluos y centrar el contenido representado en el mensaje que se quiere comunicar, atendiendo a las siguientes cuestiones:
- Presentar un solo mensaje por ayuda visual.
- Utilizar la ayuda visual para representar la información más importante.
- Escoger dos o tres aspectos clave que se quiera comunicar y representarlos por medio de distintas ayudas visuales.
Finalmente, se debe hacer un uso adecuado del color. La elección del color dependerá de los datos y del tipo de imagen. Pero deben considerarse otros tres elementos20.
- Tener en cuenta la existencia de convencionalismos asociados a alguno de los colores elegidos, así como las posibles connotaciones positivas o negativas y, en caso de que interfieran con la información que se quiere transmitir, evitarlas.
- Asegurar que cualquier posible usuario de la ayuda visual pueda comprender el mensaje con los colores utilizados. Por ejemplo, los daltónicos tienen dificultades para distinguir entre algunos colores. El caso más común es el rojo-verde. Si se utiliza el rojo y verde para mostrar una diferencia entre dos tipos de áreas, los daltónicos no lo distinguirán adecuadamente.
- Si hay relativamente pocas clases de datos para los valores en una escala continua, se considerará el uso de diferentes tonalidades del mismo color en vez de colores diferentes. Si los datos a representar son discretos o con valores positivos y negativos, se utilizarán diferentes colores.
2.2.2.3. Consideraciones sobre el tipo de gráfico a utilizar
Para escoger el tipo de gráfico adecuado es fundamental conocer el objetivo de la comunicación. Por ejemplo, no se utilizará el mismo gráfico si queremos comunicar datos sobre supervivencia o presentar la comparación de los riesgos asociados a dos tratamientos. A continuación, se detallan los tipos de gráfico más adecuados según el objeto de la comunicación:
a) Comparar distintos datos: Gráfico de barras.
El gráfico de barras clásico utiliza barras horizontales o verticales (gráfico de columnas) para mostrar comparaciones numéricas discretas entre categorías (variables cualitativas). Un eje del gráfico muestra las categorías específicas que se comparan (por ejemplo, tipos de intervención o intervención y comparador) y el otro eje representa una escala de valores (por ejemplo, niveles de presión arterial). Los datos de los gráficos de barras son datos categóricos y, por lo tanto, responde a la pregunta de «¿cuántos?» en cada categoría. En la figura 2.2.2. se puede ver un ejemplo de gráfico de barras usado para comparar los efectos en la presión arterial de distintos fármacos y placebo en dos grupos de población.
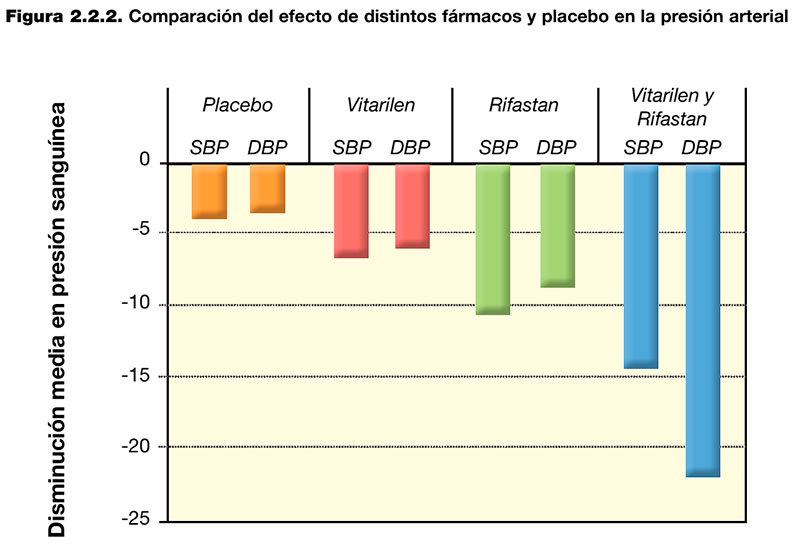
b) Representar tendencias en un periodo de tiempo: Gráfico de líneas.
Los gráficos de líneas se utilizan para mostrar valores cuantitativos en un intervalo continuo. Habitualmente, en el eje Y (vertical) se representa un valor cuantitativo (por ejemplo, variación en la presión arterial sistólica) y en el eje X (horizontal) se representan categorías o secuencias (por ejemplo, meses de tratamiento). En la figura 2.2.3. se puede ver un ejemplo de gráfico de líneas utilizado para mostrar los cambios en la presión sistólica de tres opciones terapéuticas distintas a lo largo de tres meses.
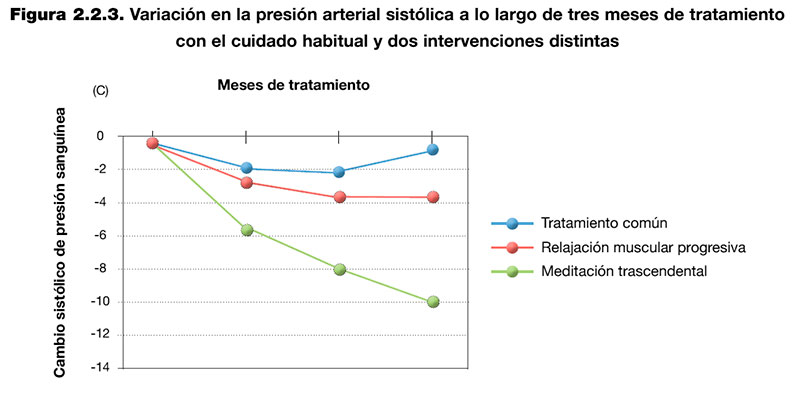
c) Comunicar información sobre proporciones: Gráfico circular de sectores.
Los gráficos circulares de sectores ayudan a mostrar proporciones y porcentajes entre categorías. Cada longitud de arco representa una proporción de cada categoría, mientras que el círculo completo representa la suma total de datos, igual al 100%. En la figura 2.2.4. se muestra un ejemplo de gráfico circular de sectores para representar la frecuencia con la que se presentan distintos tipos de comorbilidades asociadas a una condición.
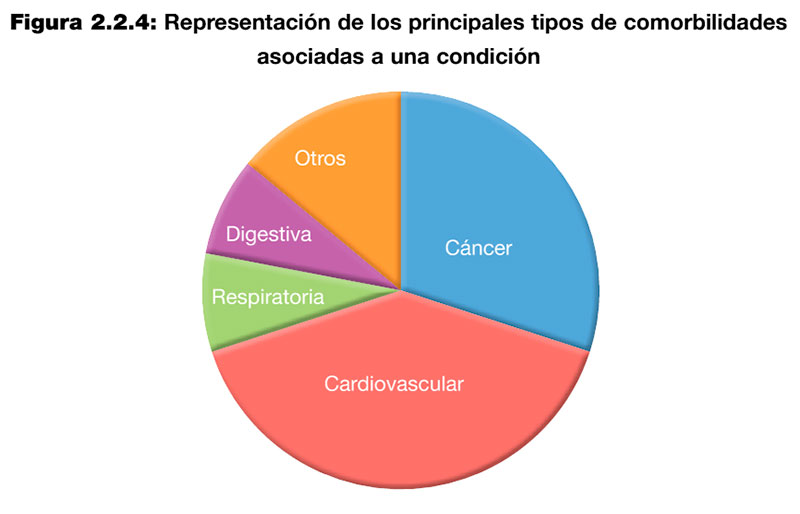
d) Representar números muy grandes: Cuadrículas
Este tipo de gráfico se sirve de cuadrículas para la visualización fraccionada del número. Así, se representan de la misma manera las unidades, decenas, centenas, unidades de mil, etc. que lo componen. En la figura 2.2.5. se representa por medio de cuadrículas el número 2.259.

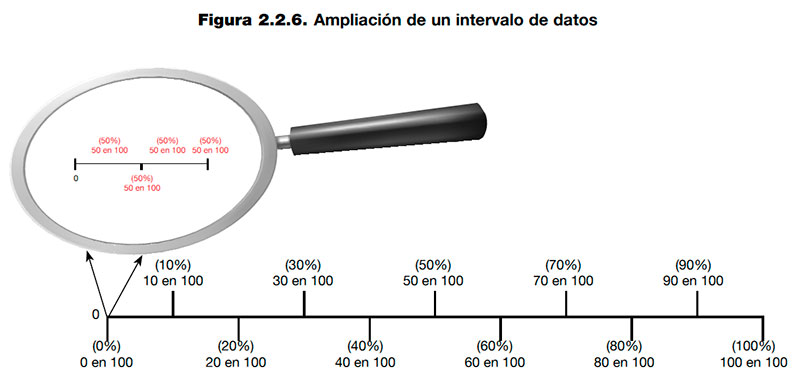
e) Representar números muy pequeños: Escala con ampliación
La ampliación de una escala proporciona el detalle de un intervalo pequeño de datos que se ubica en una escala mayor. En la figura 2.2.6. se puede ver un ejemplo de la ampliación visual de una escala.
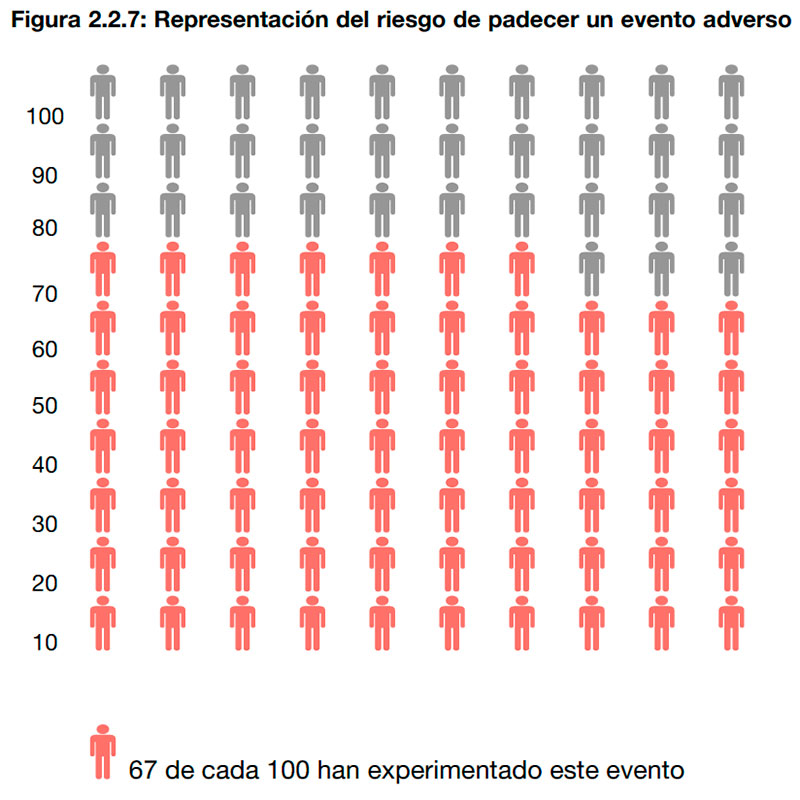
f) Comunicar la reducción del riesgo debido a un tratamiento o el riesgo de aparición de efectos secundarios: Conjunto de iconos.
En los conjuntos de iconos se muestran datos discretos en unidades (iconos), cada uno coloreado o diferenciado por medio de un color o una señal, utilizados para representar una categoría particular y agrupados en una matriz. En la figura 2.2.7. se representa el riesgo de padecer un evento adverso. En ella, aparecen coloreados de rojo aquellos individuos que, de cada grupo de población de 100 personas, sufrirían al evento adverso. De esta manera se plasma visualmente el riesgo de padecer el evento.
Recomendaciones para facilitar la comunicación de riesgo mediante el uso de iconos
Al utilizar iconos para la representación de población es conveniente tener en cuenta las siguientes recomendaciones:
- Utilizar distintos conjuntos de iconos para representar el riesgo basal (sobre la muestra de individuos no tratados) y el riesgo incremental debido al tratamiento (sobre la muestra de individuos tratados).
- Representar los individuos afectados (numerador) y la población en riesgo (denominadores).
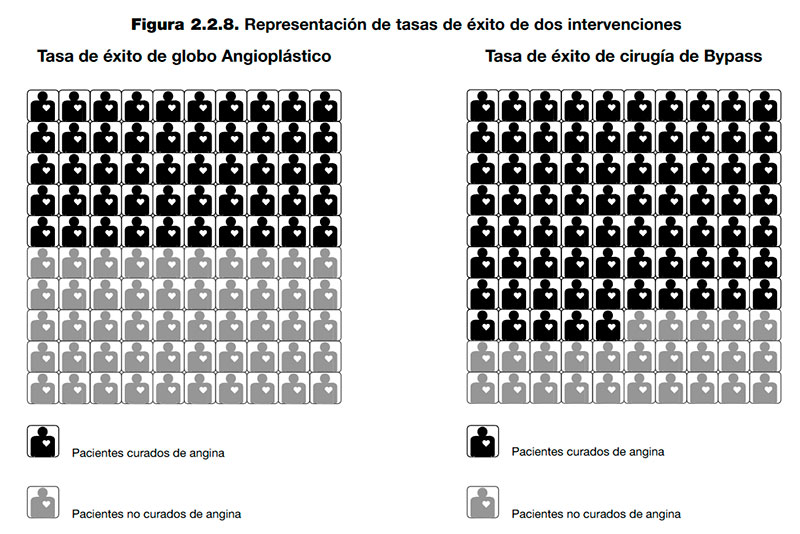
- Al comparar los riesgos o tasas de éxito, utilizar denominadores (población en riesgo) de la misma magnitud en los grupos de individuos de intervención y de comparación. En la figura 2.2.8. se puede ver una representación gráfica con denominadores de la misma magnitud.
- Colocar los iconos que representan a los individuos que se quiere diferenciar (por ejemplo, los individuos afectados) agrupados en bloque, no distribuidos aleatoriamente.
- Tener en consideración que la distribución aleatoria de los iconos puede dificultar la comprensión de lo que se está intentando transmitir, dado que requiere un análisis más elaborado de la imagen.
- Utilizar iconos que se asemejen a una persona, siempre y cuando sea posible.
- Si un riesgo es claramente mayor para un género, se recomienda representarlo con ese género. En caso contrario, se puede utilizar uno u otro sin distinción, pero no siempre el mismo.
2.2.3. Estrategias para mejorar la comunicación de datos numéricos a profesionales y pacientes
Comunicar eventos inciertos, como la previsible evolución de una enfermedad o las probabilidades de éxito de un tratamiento médico está lejos de ser trivial, especialmente por las importantes repercusiones que pude tener en la vida del paciente. La correcta comunicación de los riesgos no es sólo un problema del receptor sino también del emisor de la información, lo que puede generar dificultades. Este posible problema tiene tres vertientes: 1) la correcta comprensión de la información, 2) la interpretación que hacen los pacientes de la información, incluso cuando se comprenda de manera adecuada y 3) la existencia de la posibilidad de persuasión de cara a las acciones que tomarán paciente y profesional sanitario posteriormente. A continuación, se indican algunos de los problemas más comunes en la comunicación de riesgos médicos y se muestran algunos ejemplos clarificados, así como la evidencia existente sobre posibles soluciones.
2.2.3.1. El encuadre en la presentación de resultados
El encuadre o efecto marco (en inglés framing effect) es un sesgo cognitivo por el cual las preferencias de una persona ante un problema de decisión varían en función de cómo se presenta la información, es decir, del marco21. Se trata de una de las formas clásicas de influir sobre la percepción de los datos. Los estudios de los efectos del encuadre sobre las decisiones se han centrado en encuadre negativo respecto al positivo y encuadre de ganancias respecto de pérdidas. Un ejemplo sencillo de encuadre positivo o negativo sería un resultado con una probabilidad del 97% de supervivencia o un 3% de mortalidad.
Ambas formas de presentar la información son objetivamente equivalentes, pero informar a una persona de una probabilidad como posible beneficio sobre su salud, o en detrimento de ella afecta a las emociones de distinta manera y tiene un impacto en la toma de decisiones22. La existencia de efectos de encuadre abre la puerta a la posible manipulación hacia los pacientes, al poder presentar de una manera u otra la información para persuadirles y que, finalmente, tomen la decisión que el facultativo considera la apropiada.
La evidencia muestra que el encuadre positivo es más efectivo que el negativo cuando se trata de persuadir a las personas a escoger opciones de tratamiento más arriesgadas. Además, el encuadre de ganancias respecto a pérdidas ha demostrado tener una gran influencia sobre las decisiones de pruebas diagnósticas. Por contra, el encuadre negativo se centra en las potenciales pérdidas de no someterse a una prueba diagnóstica, como puede ser la pérdida de la salud o la longevidad. El encuadre de pérdidas ha demostrado incrementar el número de personas que se someten a las pruebas de cribado como la mamografía respecto al encuadre de ganancias como el mantenimiento de una buena salud23. Estos resultados pueden explicarse por el concepto psicológico de aversión a la pérdida (loss aversion), según el cual sufrimos el doble por una pérdida de un determinado valor que lo que disfrutamos por una ganancia de una cantidad equivalente. No obstante, una revisión sistemática de la literatura sobre el efecto encuadre concluye que su efecto en cada circunstancia puede ser muy distinto24.
Un ejemplo clásico es un estudio que se realizó hace varias décadas en el que se ofrecía a los pacientes dos tratamientos para el cáncer: uno en el que se presentaban los beneficios como supervivencia a 1 y 5 años y otro en el que las mismas probabilidades se presentaban como mortalidad en el mismo periodo de tiempo. El encuadre conseguía invertir las preferencias de los pacientes entre los dos tratamientos fue independiente de que quienes expresaban sus preferencias entre los dos tratamientos fueran pacientes o médicos25.
Dado que a día de hoy no está clara la mejor estrategia para evitar el encuadre, hasta disponer de evidencia más clara, esta cuestión se puede resolver de forma práctica haciendo una doble presentación que incluya la información utilizando tanto el encuadre positivo como el negativo. Es decir, tanto de la efectividad como del fracaso terapéutico, ya que parece que cuando se presenta la información completa el efecto tiende a desaparecer26.
2.2.3.2. Comunicación por medio de descriptores verbales y numéricos
Las palabras tienen diferentes significados para las distintas personas y, por lo tanto, su interpretación puede ser ambigua. En la comunicación de riesgos la utilización de términos vagos como «algunas veces» o «frecuentemente» inducen a error porque los receptores interpretan de forma diferente la frecuencia que estas palabras quieren expresar27.
Cuando el prospecto de un medicamento informa de que un efecto adverso es «frecuente» se refiere, y así lo explícita, a una frecuencia del 1-10%. Sin embargo, un estudio ha mostrado que cuando a una persona se le informa que un efecto adverso es «frecuente» ésta estima que ocurre en el 50% de las ocasiones, y en un 25% si se trata de un profesional sanitario28,29.
Se recomienda priorizar el uso de descriptores numéricos respecto a los verbales ya que la posible ambigüedad en la interpretación de éstos podría llevar a sobrestimar los riesgos y afectar a la toma de decisiones. En esta línea y con el objetivo de comunicar resultados a profesionales y pacientes de una forma más clara, una reciente publicación GRADE propone una plantilla con la que formular recomendaciones en base a resultados de revisiones sistemáticas de acuerdo con el tamaño del efecto y el grado de certeza de la evidencia30.
2.2.3.3. Comunicación de probabilidades de eventos
Para la presentación de la probabilidad de un evento generalmente se utilizan frecuencias simples (20 de cada 100) o porcentajes (20%) pero las personas tienden a atribuir distintos riesgos a probabilidades equivalentes presentadas en esos dos formatos.
A continuación, se presentan los diferentes sesgos a la hora de presentar la información en frecuencias o porcentajes27:
- Cuando el riesgo se presenta como frecuencias simples tiende a ser magnificado respecto a cuándo se presenta su porcentaje equivalente, especialmente en pacientes con baja destreza aritmética.
- Es frecuente interpretar un 20% como 1 de cada 20.
- La presentación de diferentes resultados en frecuencias que utilizan distintos denominadores dificulta la comprensión y eleva la percepción del riesgo.
- Evitar la presentación de resultados en formatos 1 de cada X ya que dificulta la comparación entre los diferentes riesgos presentados.
- Las frecuencias expresadas con denominadores bajos (100) son más fáciles de interpretar que las de números más elevados (10.000) ya que los números altos son más complicados de memorizar.
- La presentación de la información con decimales, sin redondear a número entero, dificultan la interpretación.
- Cuando los riesgos son muy bajos intuitivamente se tiende a interpretar que la probabilidad es muy pequeña, cercana a cero.
Para evitar estos sesgos generalmente se recomienda presentar las probabilidades en números enteros, sin decimales, utilizando denominadores bajos y siendo consistentes en la forma de presentar la información a lo largo del texto. Algunos autores sugieren la utilización tanto de porcentajes como de frecuencias de manera simultánea27,31 sin embargo no hay evidencia de que ese uso mejore la interpretación de los resultados.
Además de los sesgos identificados en la presentación de probabilidades, para una presentación óptima de la información es necesario tener en cuenta si se trata de probabilidades de eventos únicos o múltiples o probabilidades condicionadas tal como se explica a continuación.
a) Comunicación de probabilidades de evento único
«Mañana hay 30% de probabilidad de lluvia» es una probabilidad de evento único.
«Si toma este antidepresivo tiene una probabilidad del 30%-50% de presentar un efecto adverso sexual» es una probabilidad de un evento único, que sin embargo tiene una interpretación ambigua.
La probabilidad en este caso se refiere a un evento único y concreto, pero las personas generalmente pensamos en términos de clases de eventos y si no se nos explicita la clase a la que se refiere es probable que cada uno construya su propia referencia generando confusión y distintas interpretaciones32. En este sentido, un estudio ha observado que los facultativos relacionan el dato con los pacientes, mientras que los pacientes lo relacionan con su propia experiencia. De esta manera, unos interpretaron que el 30-50% de los pacientes tendría problemas sexuales, otros que tendrían problemas en el 30-50% de sus relaciones sexuales y algunos incluso que tendrían relaciones sexuales que resultarían ser un 30-50% menos satisfactorias32.
Este problema se puede evitar utilizando frecuencias simples en lugar de porcentajes. De esta forma, transformar el mensaje «si toma este medicamento tiene un 30-50% de probabilidades de tener un problema sexual» a «de los 10 pacientes a los que se prescribe este antidepresivo, entre 3 y 5, presentan un problema sexual» facilita la interpretación del riesgo32.
Para la presentación de probabilidades de evento único es importante definir el denominador y dejar clara la clase de evento al que se está haciendo referencia para evitar malinterpretaciones.
b) Comunicación de probabilidades de eventos múltiples
La presentación de los resultados de eficacia de los medicamentos A, B y placebo en un ensayo clínico es una probabilidad de evento múltiple. La presentación de esta información en la que un paciente debe elegir entre el medicamento A o B puede producir saturación de información y es importante simplificar su recepción.
En estos casos se considera más apropiado expresarlo así: la probabilidad de resolución con el tratamiento A es de 15%, con el B del 30% y con un placebo del 5%, que decir que los medicamentos son eficaces en 1,5% de cada 10 casos (A), 3 de cada 10 (B) y 0,5 de cada 10 (placebo)32.
Para comparar resultados de probabilidades de eventos múltiples, se recomienda expresarlos como porcentajes ya que facilitan la comparación respecto a la presentación de la información como frecuencias naturales.
c) Comunicación de probabilidades condicionadas
La probabilidad de tener un cáncer de mama dependiendo del resultado de una mamografía y teniendo además en cuenta la sensibilidad y especificidad de la prueba es una probabilidad condicionada. Este tipo de probabilidades requiere aplicar la regla de Bayes, que implica realizar tres multiplicaciones y dificulta, independientemente de si se trata de profesionales sanitarios o pacientes, obtener un valor predictivo positivo33.
En un congreso médico se presentó a los 160 ginecólogos asistentes los siguientes datos tras varios estudios en los que se investigaron las probabilidades conjuntas33:
- La probabilidad de que una mujer tenga cáncer de mama es de un 1%.
- En mujeres con cáncer de mama la probabilidad de un resultado positivo en una mamografía es del 90%.
- En mujeres que no tienen cáncer mama la mamografía puede dar positivo en un 9% de los casos.
Posteriormente se les preguntó la probabilidad de que un paciente que dé positivo en una mamografía tenga realmente un cáncer de mama, presentando cuatro posibles respuestas. La mayoría de los ginecólogos no supo calcular la respuesta correcta y hubo una gran heterogeneidad entre las respuestas. Por el contrario, cuando se presenta la misma información, pero se expresa como frecuencias naturales es mucho más sencillo reconocer la respuesta:
- Prevalencia: 10 de cada 1000 mujeres tienen un cáncer de mama.
- Sensibilidad: de estas 10 mujeres con cáncer de mama, a 9 se lo detectaron en una mamografía.
- Especificidad (falsos positivos): de las 990 mujeres sin cáncer de mama, a 89 de ellas la mamografía les indica que tienen un cáncer de mama.
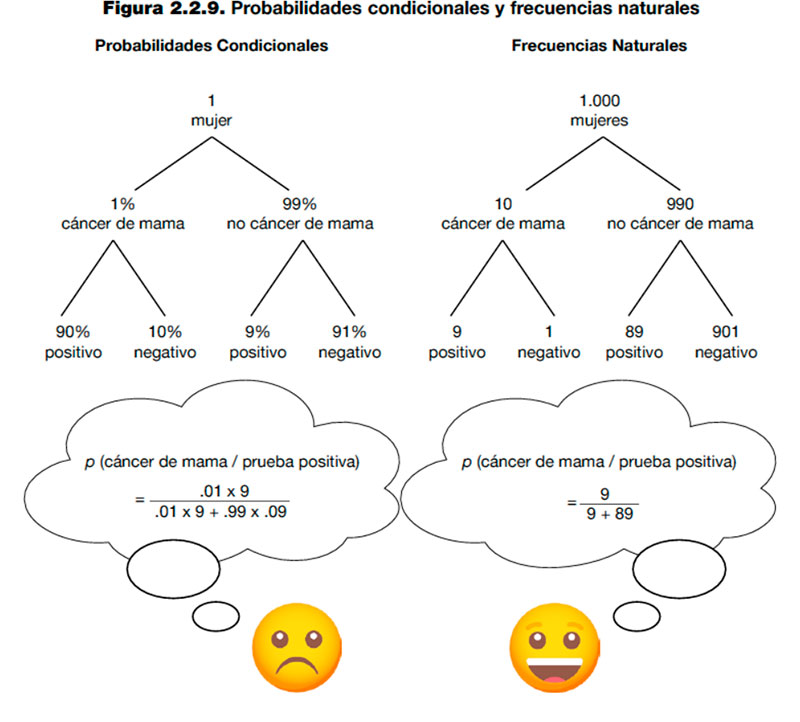
Mostrando la información de esta otra forma, utilizando frecuencias naturales y no probabilidades, es casi inmediato darse cuenta de que de las 98 mujeres a las que la mamografía indica que tienen un cáncer de mama, sólo 9 de ellas realmente lo tienen, lo que quiere decir que el 90% de las mujeres a quienes la mamografía les indica que tienen un cáncer de mama no lo tienen. Por tanto, la respuesta correcta a la vista de los datos objetivos es que la probabilidad de tener cáncer de mama habiendo dado resultado positivo en una mamografía es sólo del 10%.
Una revisión sistemática ha mostrado que las frecuencias naturales facilitan la compresión, respecto a las probabilidades condicionales, en el contexto de presentación de resultados de cribado o pruebas diagnósticas sin que se hayan encontrado diferencias en función de si se trata de profesionales o pacientes34.
Se recomienda informar sobre probabilidades conjuntas utilizando frecuencias naturales y no porcentajes ya que resultan más intuitivas y facilitan los cálculos a realizar.
2.2.3.4. Comunicación de cambios en resultados numéricos
En general, la comunicación de los cambios generados por una intervención, como pueden ser los efectos de un tratamiento o los cambios en la salud a largo plazo, se expresan como cambios en las probabilidades. Para presentar esta información se utilizan las medidas de riesgo como el riesgo absoluto (RA), riesgo relativo (RR) o cuando se presentan las diferencias entre las dos intervenciones se expresan como reducciones del riesgo. Otra forma de presentar esta información es a través del NNT (número necesario a tratar) (ver glosario). El NNT es una medida de riesgo que se introdujo en los años 80 con una gran aceptación entre los profesionales ya que su interpretación clínica resultaba más intuitiva.
Es sabido que la presentación de los riesgo como RR sobreestima los resultados en comparación con la presentación como RA, especialmente si el riesgo basal es pequeño. Esto ha sido tradicionalmente utilizado para persuadir, presentando datos de aparentemente mayor impacto, lo que en ocasiones ha tenido una gran repercusión social34. En el año 1996, por ejemplo, una comunicación gubernamental oficial del Reino Unido alertaba de que la píldora anticonceptiva de segunda generación duplicaba el riesgo de sufrir un tromboembolismo venoso. Esta información causó una gran preocupación entre las mujeres, provocó la disminución del uso de anticonceptivos y tuvo un impacto sobre el número de embarazos y abortos, en los que se estimó un exceso de entre 12.000 y 14.000 casos. La información proporcionada a las mujeres utilizaba el RR alertando de que el riesgo se duplicaba. Teniendo en cuenta que el riesgo basal era muy bajo (1 de 7.000) y que con la nueva píldora el riesgo pasaba al 2 de 7.00035, si se hubiera proporcionado esta información, muchas mujeres no hubieran tomado la misma decisión.
Una revisión sistemática ha mostrado que presentar la información como RR hace que, tanto pacientes como profesionales sanitarios, perciban las intervenciones como más efectivas o sean más persuasivas de cara a prescribir o aceptar una intervención que cuando los resultados se presentan como RA o NNT34. En este sentido, la utilización de RR, tiende a desinformar de cara a la toma de decisiones, especialmente cuando el riesgo basal es bajo, y no informar del mismo tiende a exagerar la percepción de diferencia. Por otra parte, los estudios muestran que profesionales y pacientes perciben las intervenciones como más efectivas y comprenden mejor los resultados cuando se presenta como RA que cuando lo hacen como NNT. Sin embargo, no se han encontrado diferencias en relación a la capacidad de persuasión para prescribir o aceptar un medicamento.
Se recomienda presentar los cambios en los resultados a través del RA ya que la utilización de RR y NNT es más persuasiva y difícil de comprender respectivamente. Una variante es presentar el riesgo incremental, que supone presentar los riesgos absolutos acompañados del riesgo basal. El riesgo incremental funciona mejor cuando se acompaña de ayudas visuales. En caso de que sea necesario presentar el RR se recomienda acompañarlo del riesgo basal.
2.2.3.5. Comunicación de estimaciones personalizadas de riesgo
Los estudios sugieren que cuando la información de un riesgo se personaliza, se produce un incremento de la percepción del riesgo y mejora el conocimiento, al contrario que cuando la información se presenta de forma genérica. En todo caso la evidencia es limitada y presenta resultados heterogéneos que generan dudas razonables sobre si presentar información personalizada o diseñada «a medida» verdaderamente tiene impacto sobre las decisiones sobre la salud.
La mayor parte de la investigación realizada en estimaciones personalizadas de riesgo se ha centrado en el cribado de cáncer, donde han demostrado incrementar el número de participantes activos en, por ejemplo, el cribado de cáncer de mama y de cérvix36. Un meta-análisis ha mostrado que las estimaciones personalizadas de riesgo son efectivas para los cambios de hábitos, pero, sin embargo, el tamaño del efecto es muy pequeño37.
De momento, no es posible hacer recomendaciones sobre la información personalizada del riesgo ya que todavía no se conoce con exactitud cómo afecta a la compresión ni su impacto sobre la toma de decisiones27.
2.2.3.6. Comunicación de resultados a largo plazo
Los pacientes están interesados en disponer de información a largo plazo de los resultados de las intervenciones a las que se someten. A las dificultades propias de disponer de este tipo de datos, los ensayos clínicos suelen incluir un seguimiento de tan sólo 1-2 años, debemos añadir las propias de presentar datos a largo plazo, así como de forma comprensible. Existen distintas maneras de presentar este tipo de resultados27:
- Probabilidad de un evento en un momento específico en el tiempo. Se utiliza por ejemplo para presentar los beneficios cardiovasculares a 10 años de medicamentos como los antiagregantes y estatinas.
- Probabilidad de un evento en varios momentos a lo largo del tiempo. Por ejemplo, la probabilidad de tener que repetir un by-pass a los 5 o 10 años de la primera intervención.
- Curvas de mortalidad o supervivencia utilizadas habitualmente en la presentación de beneficios de los programas de cribado de cáncer.
- Probabilidad acumulada de un evento en el tiempo como las empleadas habitualmente para la presentación de riesgo de cáncer de mama en pacientes con mutaciones del gen BRCA.
- La incidencia de un evento que es constante en el tiempo se utiliza para representar el riesgo anual de embarazo en pacientes en tratamiento con un método anticonceptivo específico.
En las pruebas de cribado, una de las formas de presentar resultados a largo plazo es la supervivencia a los 5 años. Sin embargo, puede confundir y llevar a interpretar erróneamente que un aumento en la tasa de supervivencia implica salvar vidas. A pesar de que intuitivamente parece imposible que una intervención que aumente la supervivencia no implique reducciones de mortalidad, es una confusión frecuente generada por dos sesgos cognitivos, el sesgo temporal y el sobrediagnóstico. El sesgo temporal en el cribado implica que, aunque con esta intervención somos capaces de detectar el tumor precozmente, no se consigue necesariamente una reducción de la mortalidad ya que puede significar vivir más tiempo con un diagnóstico positivo de la enfermedad, pero no vivir más años (ver figura 2.2.10).

La segunda dificultad está en el sobrediagnóstico, las pruebas de cribado permiten detectar tumores que encajan en la definición patológica de cáncer pero que presentan un crecimiento muy lento o no progresan y que por tanto no hubieran provocado la muerte38. Tal como se muestra en la figura 2.2.11, cuanto mayor es el sobrediagnótico también se observa una mayor tasa de supervivencia, pero sin que ello implique una reducción de la mortalidad.

La investigación relativa a la presentación de resultados de cribado en tasas de supervivencia ha mostrado que no solo confunde a pacientes, sino también a médicos e incluso a editores de revistas médicas38. En un estudio de 3 de cada 4 médicos encuestados creía, erróneamente, que en el cribado las tasas de supervivencia a 5 años podrían demostrar reducciones de la mortalidad, cuando la realidad es que solo se puede demostrar que una intervención salva vidas a través de tasas de reducción de la mortalidad39.
No se dispone de ensayos clínicos que hayan estudiado el efecto de las diferentes formas de presentación de riesgos a largo plazo y, por tanto, de momento no es posible hacer recomendaciones en esta línea. Hasta que se cuente con resultados más robustos, parece que la opción más práctica es elegir la representación que mejor se adapte al tipo de información que es necesario presentar.
En relación con la presentación de resultados de beneficios a largo plazo del cribado, se recomienda utilizar tasas de mortalidad, ya que las tasas de supervivencia a 5 años pueden inducir a confusión creando la ilusión de una reducción de la mortalidad cuando realmente no existe como tal. En el caso concreto de las campañas de cribado de cáncer no se debe perder de vista que el objetivo principal es proporcionar la mejor información a los pacientes para la toma de decisiones más que aumentar el número de participantes en la propia campaña.
2.2.3.7. Comunicación de la incertidumbre
En medicina existe un alto grado de incertidumbre. La estimación numérica del riesgo es una expresión matemática, pero ninguna probabilidad es capaz de predecir lo que ocurrirá en un paciente en concreto. Tan solo somos capaces de mostrar la información recopilada de lo que ha ocurrido en pacientes similares en el pasado. La incertidumbre se puede dividir en dos tipos: a) aleatoria: refleja la indeterminación de los hechos futuros o b) epistémica: refleja las limitaciones en la confianza, credibilidad o adecuación de la información sobre los riesgos. Comprender este tipo de incertidumbres es esencial para la toma de decisiones27.
La comunicación de la incertidumbre aleatoria se ha valorado en pequeños estudios, los que han mostrado que no tiene un efecto significativo en la percepción del riesgo. La comunicación de la incertidumbre epistémica, estudiada a partir de la utilización de intervalos de confianza, ha mostrado tener también un efecto muy limitado sobre la percepción del riesgo, aunque sí que podría incrementar la preocupación del paciente27.
A día de hoy, no se dispone de una evidencia clara y son necesarios más estudios para determinar el papel de la comunicación sobre la incertidumbre en las percepciones del paciente, su compresión y la toma de decisiones. Se ha de ser sincero y comunicar de forma clara y tan precisa como sea posible la incertidumbre asociada a los distintos procedimientos a los que se enfrenta un paciente. Intuitivamente parece que la comunicación de la incertidumbre podría generar desconfianza y generar aversión, pero los resultados preliminares de algunos estudios sugieren que la relación y la confianza médico-paciente podrían no verse afectadas en gran medida27.
2.2.3.8. Presentación narrativa de la probabilidad de un evento
En ocasiones la información que se presenta a los pacientes incorpora, como apoyo a los datos, los testimonios de otros pacientes27. La experiencia de un paciente contiene una gran cantidad de detalles sobre lo que supone experimentar una enfermedad o someterse a un tratamiento en primera persona y han demostrado ser de utilidad en iniciativas como patients like me o en los programas de paciente experto40.
La utilización de narrativas afecta a la percepción del riesgo e influye en la toma de decisiones como por ejemplo en la intención de vacunación. En estudios con medicamentos, complementar la información con testimonios de los pacientes ha mostrado disminuir la incidencia de efectos adversos, pero, sin embargo, aumentar la gravedad de los que se presentan27. Las narrativas también han demostrado afectar a las decisiones sobre cirugía electiva, por ejemplo, el grupo de pacientes que conocieron las experiencias de otros pacientes sometidos a cirugía de by-pass presentó una mayor probabilidad de optar por operarse que el grupo que no escuchó los relatos27.
Aunque la utilización de narrativas ha demostrado afectar a la percepción del riesgo e influir en la toma de decisiones, se recomienda utilizarlas con precaución hasta que se conozca con exactitud el alcance de su impacto, especialmente en aquellas situaciones en las que se busca persuadir con el objetivo de inducir un cambio de hábitos. En caso de que se utilicen para presentar información sobre beneficios y riesgos, se debe acompañar de información en forma de pictogramas26.
2.2.3.9. Contexto de estimaciones numéricas y etiquetas evaluativas
Tradicionalmente, la comunicación de riesgos se ha apoyado en las estimaciones numéricas de las probabilidades. Sin embargo, tal y como se ha expuesto a lo largo de este capítulo, los pacientes tienen dificultades para interpretar esta información. La evidencia muestra que proporcionar a los datos contextualizados, es decir, acompañados de datos comparativos etiquetas evaluativas o símbolos ayuda a mejorar su interpretación41.
En estudios en los que se ha interpretado el resultado indicando por ejemplo si el resultado es malo, bueno o excelente, se ha comprobado que los pacientes han incorporado la utilización de esta información para la toma de decisiones. También se ha estudiado que la utilización de símbolos como estrellas, puntos de colores o marcas de visto (tic) puede ayudar a interpretar la información. Para facilitar la ponderación, la evaluación y la interpretación del valor numérico de un riesgo se han utilizado comparaciones, por ejemplo, mostrando también el resultado del paciente medio41.
Dado que los estudios en este campo han mostrado resultados inconsistentes en relación a cómo afectan a la toma de decisiones, aunque se ha confirmado que presentan capacidad para persuadir, se recomienda seleccionar con mucha cautela el contexto en con el que se presentará la información41.
Conclusión
La clave en la presentación de probabilidades de los beneficios y riesgos de las distintas intervenciones en los instrumentos de ayuda a la toma de decisiones supone la presentación de información numérica con formatos de riesgo consistente que permita la comparación de las distintas opciones y sus resultados. En ocasiones será necesario encontrar un equilibrio entre los pros y contras de utilizar un determinado formato, sin embargo, la decisión debe ir orientada a presentar la información de forma consistente y no sesgada41.
Se recomienda testar los formatos empleados con el usuario final, especialmente en aquellas ocasiones en las que se utiliza información contextual y etiquetas evaluativas o cuando las habilidades de los pacientes son limitadas41.
A pesar de que todavía hay determinadas áreas en las que es necesaria más investigación para poder ofrecer directrices claras, es necesario conocer cómo los diferentes formatos pueden afectar a la percepción del riesgo para evitar persuadir accidentalmente a los pacientes hacia una opción determinada.
Resumen de los aspectos clave
Recursos
- Harding Center for Risk Literacy.
- Université Laval Decision Box.
- Mayo Clinic Shared Decision Making National Resource Center
- DynaMed Shared Decisions. Option Grid.
- Cate’s Plot.
- The Ottawa Hospital. Patient Decision Aids.
- Dr. Chris Cates’ EBM Website – Evidence Based Medicine, NNT, Visual Rx & The Cates Plot at Dr Chris Cates EBM Website [Internet]. [citado 10 de mayo de 2021]. Disponible en: http://www.nntonline.net/.
Bibliografía 2. La TDC derivada de las recomendaciones de las GPC / 2.2. Comunicación de Resultados Numéricos para la Toma de Decisiones Compartida
1. Ratzan SC, Parker RM. Introduction. In: Selden CR, Zorn M, Ratzan SC, Parker RM, editors. National Library of Medicine current bibliographies in medicine: Health literacy. Bethesda, MD: National Institutes of Health; 2000. (NLM Pub. No. CBM 2000-1).
2. Institute of Medicine (US) Committee on Health Literacy. Nielsen-Bohlman L, Panzer AM, Kindig DA, editores. Health Literacy: A Prescription to End Confusion [Internet]. Washington (DC): National Academies Press; 2004 [citado 22 febrero 2021]. Disponible en: https://www.nap.edu/catalog/10883/health-literacy-a-prescription-to-end-confusion#toc.
3. Gigerenzer G, Gaissmaier W, Kurz-Milcke E, Schwartz LM, Woloshin S. Helping doctors and patients make sense of health statistics. Psychological science in the public interest. 2007;8(2): 53-96.
4. Wegwarth O, Gigerenzer G. The barrier to informed choice in cancer screening: statistical illiteracy in physicians and patients. Recent Results Cancer Res. 2018;210:207-221.
5. Petrova D, Mas G, Navarrete G, Rodriguez TT, Ortiz PJ, Garcia-Retamero R. Cancer screening risk literacy of physicians in training: An experimental study. PLoS One. 2019;14(7):e0218821.
6. Reyna VF, Nelson WL, Han PK, Dieckmann NF. How numeracy influences risk comprehension and medical decision making. Psychol Bull. 2009;135(6):943-73.
7. Kickbusch I, Pelikan JM, Apfel F, Tsouros AD, Eds. Health literacy: The solid facts [Internet]. Copenhagen: World Health Organization; 2013 [citado enero 2022]. Disponible en:
https://www.euro.who.int/__data/assets/pdf_file/0008/190655/e96854.pdf.
8. Spiegelhalter D, Pearson M, Short I. Visualizing uncertainty about the future. Science. 2011 Sep 9;333(6048):1393-400.
9. Ancker JS, Senathirajah Y, Kukafka R, Starren JB. Design features of graphs in health risk communication: a systematic review. J Am Med Inform Assoc. 2006;13(6):608-18.
10. Hildon Z, Allwood D, Black N. Making data more meaningful: patients’ views of the format and content of quality indicators comparing health care providers. Patient Educ Couns.
2012;88(2):298-304.
11. Lipkus IM, Hollands JG. The visual communication of risk. J Natl Cancer Inst Monogr. 1999;25:149-63.
12. Edwards A, Elwyn G, Mulley A. Explaining risks: turning numerical data into meaningful pictures. BMJ. 2002;324(7341):827-30.
13. Garcia-Retamero R, Cokely ET. Communicating health risks with visual aids. Current Directions in Psychological Science. 2013;22(5):392-399.
14. Garcia-Retamero R, Cokely ET. Using visual aids to help people with low numeracy make better decisions. Numerical reasoning in judgments and decision making about health. 2014; 153-174.
15. Mazur DJ, Hickman DH. Patient preferences: survival vs quality-of-life considerations. J Gen Intern Med. 1993;8(7):374-7.
16. Shah P, Hoeffner J. Review of graph comprehension research: Implications for instruction. Educational psychology review. 2002;14(1):47-69.
17. Okan Y, Garcia-Retamero R, Cokely ET, Maldonado A. “Individual differences in graph literacy: Overcoming denominator neglect in risk comprehension.” Journal of Behavioral Decision Making. 2012;25(4):390-401.
18. Okan Y, Galesic M, Garcia-Retamero R. How people with low and high graph literacy process health graphs: Evidence from eye-tracking. Journal of Behavioral Decision Making. 2016;29(2-3):271-294.
19. Garcia-Retamero R, Cokely ET. Designing visual aids that promote risk literacy: A systematic review of health research and evidence-based design heuristics. Human factors. 2017;59(4): 582-627.
20. NACIONES UNIDAS. Cómo hacer comprensibles los datos. Parte 2: una guía para presentar estadísticas. Ginebra: NACIONES UNIDAS; 2009.
21. Wilson DK, Purdon SE, Wallston KA. Compliance to health recommendations: A theoretical overview of message framing. Health Education Research. 1988;3(2):161-171.
22. Tversky A, Kahneman D. The framing of decisions and the psychology of choice. Science. 1981;211:453-8.
23. Gigerenzer G, Edwards A. Simple tools for understanding risks: from innumeracy to insight. BMJ. 2003;327(7417):741-4.
24. Akl EA, Oxman AD, Herrin J, Vist GE, Terrenato I, Sperati F, Costiniuk C, Blank D, Schünemann H. Framing of health information messages. Cochrane Database Syst Rev. 2011 Dec 7; (12): CD006777. doi: 10.1002/14651858.CD006777.pub2.
25. McNeil BJ, Pauker SG, Sox HC Jr, Tversky A. On the elicitation of preferences for alternative therapies. N Engl J Med. 1982;306(21):1259-62.
26. Gigerenzer G. Should patients listen to how doctors frame messages? BMJ. 2014;349:g7091.
27. Trevena LJ, Zikmund-Fisher BJ, Edwards A, Gaissmaier W, Galesic M, Han PK, et al. Presenting quantitative information about decision outcomes: a risk communication primer for patient decision aid developers. BMC Med Inform Decis Mak. 2013;13 Suppl 2:S7.
28. Berry DC, Raynor DK, Knapp p. Communicating risk of medication side effects: An empirical evaluation of EU recommended terminology. Psychol Health Med. 2003;8:251-63.
29. Berry Dc, Holden W, Bersellini e. Interpretation of recommended risk terms: differences between doctors and lay people. Int J Pharm Pract. 2004;12:117-24.
30. Santesso N, Glenton C, Dahm P, Garner P, Akl EA, Alper B, et al. GRADE guidelines 26: informative statements to communicate the findings of systematic reviews of interventions. J Clin Epidemiol. 2020;119:126-135.
31. Freeman ALJ. How to communicate evidence to patients. Drug Ther Bull. 2019;57(8):119-124.
32. Gigerenzer G1, Galesic M. Why do single event probabilities confuse patients? BMJ. 2012;344:e245.
33. Gigerenzer G. What are natural frequencies? BMJ. 2011;343:d6386.
34. Akl EA, Oxman AD, Herrin J, Vist GE, Terrenato I, Sperati F, Costiniuk C, Blank D, Schünemann H. Using alternative statistical formats for presenting risks and risk reductions. Cochrane Database Syst Rev. 2011;2011(3):CD006776.
35. Furedi A. The public health implications of the 1995 ‘pill scare’. Hum Reprod Update. 1999;5(6):621-6.
36. Albada A, Ausems MG, Bensing JM, van Dulmen S. Tailored information about cancer risk and screening: a systematic review. Patient Educ Couns. 2009;77(2):155-71.
37. Noar SM1, Benac CN, Harris MS. Does tailoring matter? Meta-analytic review of tailored print health behavior change interventions. Psychol Bull. 2007;133(4):673-93.
38. Gigerenzer G, Muir Gray JA. Better Doctors, Better Patients, Better Decisions: Envisioning Health Care 2020. The MIT Press; 2011. Project MUSE.
39. Gigerenzer G, Gaissmaier W, Kurz-Milcke E, Schwartz LM, Woloshin S. Helping Doctors and Patients Make Sense of Health Statistics. Psychol Sci Public Interest. 2007;8(2):53-96.
40. Wicks P , Thorley EM, Simacek K, Curran C, Emmas C. Scaling PatientsLikeMe via a “Generalized Platform” for Members with Chronic Illness: Web-Based Survey Study of Benefits Arising J Med Internet Res. 2018;20(5):e175.
41. Bonner C, Trevena LJ, Gaissmaier W, Han PKJ, Okan Y, Ozanne E, Peters E, Timmermans D, Zikmund-Fisher BJ. Current Best Practice for Presenting Probabilities in Patient Decision Aids: Fundamental Principles. Med Decis Making. 2021; Epub ahead of print.






